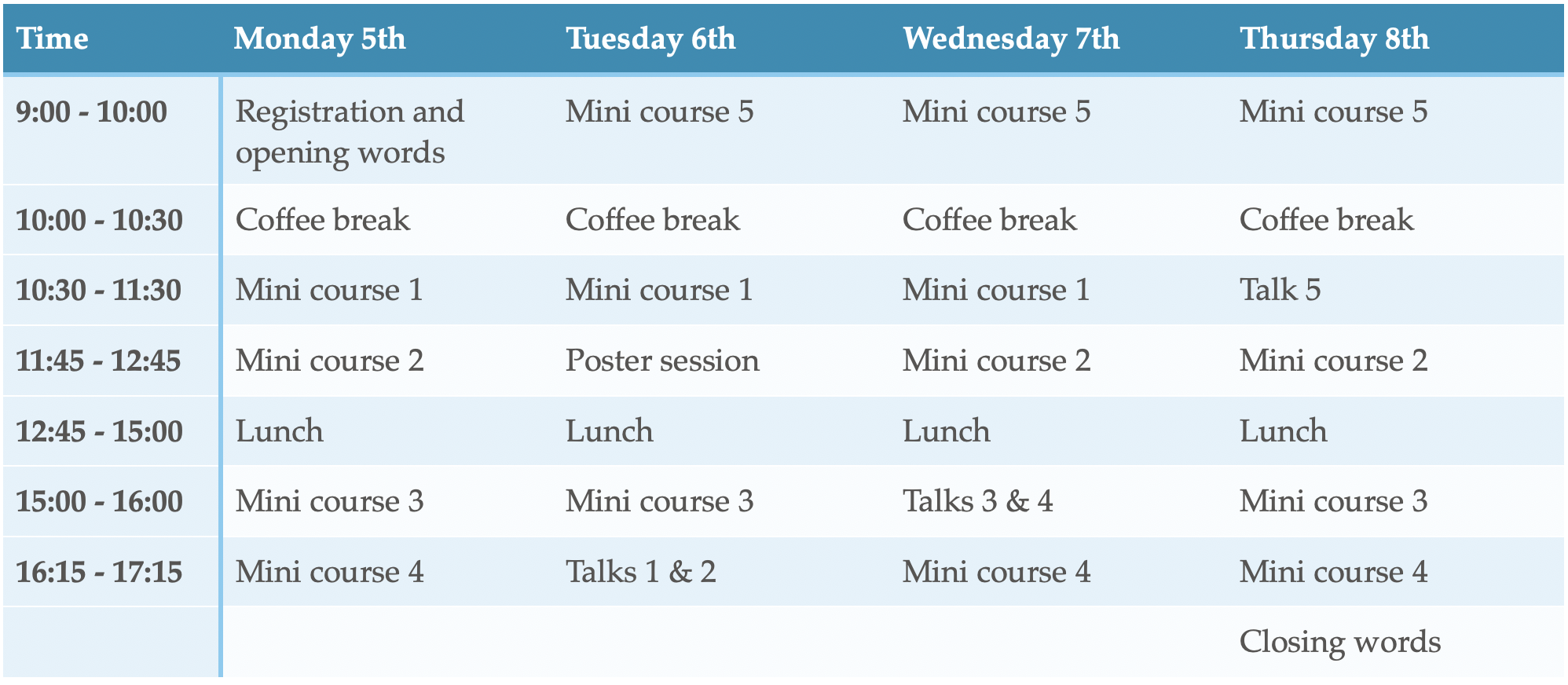
Download the program and abstracts of mini-courses and talks here.
Mini courses
Mini course 1: Mathematics of X-ray Computed Tomography. Tatiana Bubba.
Mini course 2: Perturbations of an elliptic PDE and applications to inverse problems and shape optimization. Eric Bonnetier.
Mini course 3: Introduction to the Boundary Control method. Lauri Oksanen.
Mini course 4: Optimal Control and Machine Learning. Donato Vásquez.
Mini course 5: Microlocal analysis for the geodesic X-ray transform and boundary rigidity. Andras Vasy.
Talks
Talk 1: Some applications of the finite element method in inverse problems
Speaker: Jorge Aguayo
Abstract: This talk will present some numerical results for solving elliptic optimal control problems using finite elements method and some applications in parameter identification problems. The theoretical results will be compared with numerical tests that aim to study the effect of subduction earthquakes and the detection of obstacles immersed in fluids.
Talk 2: The inverse (poro)elasticity problem in biomedicine
Speaker: Nicolás Bernafi
Abstract: The inverse elasticity problem can be simply stated as: given a deformed configuration and the forces that act on it, find an initial stress-free configuration such that when the given forces are applied to it, one recovers the given deformed configuration. Surprisingly, this problem can be framed as a (direct) elasticity one, whose mathematical properties are inherited from the original direct problem if the underlying material is sufficiently regular. In this talk, I will review this problem and its main mathematical properties. After this brief introduction, I will show some artifacts that appear when solving this problem, such as self-intersections and geometrically incompatible solutions. The talk will finish with an extension of this system to poroelastic materials, where I will show that the strong form of the equations does not allow for a weak formulation, and this requires some special treatment. All models will be shown to work in realistic heart geometries
Talk 3: Super-Resolved Multi-Slice Time-Dependent Deep Image Prior for Cardiac Cine MRI at 0.55T
Speaker: Evelyn Cueva
Abstract: Magnetic Resonance Imaging (MRI) reconstruction can be formulated as an inverse problem involving undersampled Fourier measurements. In accelerated and low-field MRI, the problem becomes severely ill-posed due to aggressive k-space undersampling, low signal-to-noise ratio, and limited spatial resolution, particularly in dynamic cardiac imaging.
This talk presents a Deep Image Prior (DIP) approach for super-resolution in accelerated low-field MRI from an inverse problems perspective. DIP acts as an implicit regularizer by parametrizing the solution through a convolutional neural network optimized directly on the measured data, without external training. We discuss the role of architectural bias and early stopping as regularization mechanisms, and introduce a multi-scale formulation that couples low- and high-resolution reconstructions. Structured latent-space modeling is used to exploit temporal and spatial redundancies, enabling coherent dynamic super-resolution in challenging MRI settings
Talk 4: Simultaneous determination of wave speed, diffusivity and nonlinearity in the Westervelt equation
Speaker: Sebastián Acosta
Abstract: The Westervelt equation models the propagation of high-intensity ultrasound waves. For medical imaging purposes, it is needed to estimate the parameters in the equation that model wave speed, diffusivity, and nonlinearity. We show that, by constructing time-periodic solutions excited from the boundary time-harmonically at a sufficiently high frequency, knowledge of the first- and second-harmonic Cauchy data at the boundary is sufficient to simultaneously determine the wave speed, diffusivity and nonlinearity in the interior of the domain of interest.
Talk 5: The fractional anisotropic Calderón problem
Speaker: Gunther Uhlmann
Abstract: We will discuss some recent progress on the anisotropic Calderón
problem for the fractional Laplacian.