Book of abstracts
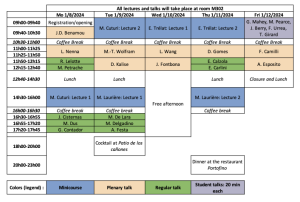
Program
Lectures
Marco Cuturi: Regularized and Neural Approaches to Solve Optimal Transport
I will present in this short course various fundamental regularized approaches (entropic, low rank, unbalanced, etc.) to solve the discrete OT problem between two samples. I will then use these tools to introduce out of sample extensions for these quantities, using e.g. entropic maps or neural network based approximations of Monge maps.
Mathieu Laurière: Learning methods in mean field games.
Mean field games (MFG) and mean field control (MFC) problems have been introduced to study very large populations of strategic agents interacting in a symmetric way. The theoretical foundations have been extensively developed, and potential applications have been proposed in a wide range of fields, from economics to sociology and engineering. Numerical methods based on classical schemes or machine learning tools have been developed. In this course, we will focus on the question of learning Nash equilibria and social optima in mean field problems. We will first discuss algorithms such as Picard iterations, Fictitious Play and Online Mirror Descent for MFG, or dynamic programming and gradient descent for MFC. We will then discuss how to incorporate model-free reinforcement learning in these methods. Numerical illustrations and sample codes will be presented.
Emmanuel Trélat: From microscopic to macroscopic scale equations: mean field, hydrodynamic and graph limits
Considering finite particle systems, we elaborate on various ways to pass to the limit as the number of agents tends to infinity, either by mean field limit, deriving the Vlasov equation, or by hydrodynamic or graph limit, obtaining the Euler equation. We provide convergence estimates. We also show how to pass from Liouville to Vlasov or to Euler by taking adequate moments. Our results encompass and generalize a number of known results of the literature.
As a surprising consequence of our analysis, we show that sufficiently regular solutions of any quasilinear PDE can be approximated by solutions of systems of N particles, to within 1/log(log(N)).
This is a work with Thierry Paul.
Plenary Talks
Jean-David Benamou: Entropic Regularisation and Martingale Optimal Transport
Given initial and final probability densities the dynamic version of Optimal Transport determines the speed vector field controlling the curve in time of probability densities that minimizes its kinetic energy. Entropic OT, aka Schroedinger problem, minimizes over the law of a random time process with prescribed initial/final marginals the relative entropy between its law and a reference measure. In full generality, the reference measure can be the law of an Ito diffusion but the relative entropy will force the two measures to
share the same support and only the drift of the optimal random time process controls the system, the diffusion part is hard-coded by the reference measure. It is known that the relative entropy between the law of discrete time diffusion, scaled by the time step,
is a “divergence” between their volatilies: freezing the reference volatility, it is positive, convex and achieves minimum at the reference volatility, and called the “specific relative entropy”. We show that the time discretisation of a martingale or semi-martigale OT problem, using the same scaling on the relative entropic penalization, allows control over the volatility according (assymptotically in the time step) to the specific relative entropy. We provide a Gamma-convergence result. From the computational point of view, the entropic penalization leads to a multi-marginal Sinkhorn solution algorithm. We describe an efficient linear cost implementation and provide numerical results supporting the
established theoretical convergence.
Fabio Camilli: A PDE approach to hard clustering
We introduce a systems of Hamilton-Jacobi equations characterizing geodesic centroidal tessellations, i.e. tessellations of domains with respect to geodesic distances where generators and centroids coincide. Typical examples are given by geodesic centroidal Voronoi tessellations in hard clustering analysis and geodesic centroidal power diagrams in semi-discrete Optimal Transport. An appropriate version of the Fast Marching method on unstructured grids allows computing the solution of the Hamilton-Jacobi system and therefore the associated tessellations. We propose various numerical examples to illustrate the features of the technique.
Antonio Esposito: Interplay between numerical methods and evolution PDEs on graphs
The talk concerns the study of evolution equations on graphs, motivated by applications in data science and opinion dynamics. One of the main differences compared to traditional ambient spaces is that vertices of the graphs, in contrast with individuals, do not move. The evolution of interest is rather that of a mass density the vertex can store. Therefore, the corresponding dynamics will differ depending on the chosen mass interpolation on vertex pairs. We will focus on nonlocal continuity equations on graphs, with emphasis on graph analogues of the continuum nonlocal-interaction equation. The graph continuity equation uses an upwind interpolation to define the density along the edges, which has both theoretical and computational advantages. However, this choice reveals a Finslerian gradient flow structure, rather than Riemannian, since the resulting Wasserstein distance on graphs is actually a quasi-metric. We will address existence of suitably defined solutions, as well as their asymptotic behaviour when the number of vertices converges to infinity and the graph structure localises. The two limits lead to different dynamics. Finally, we will discuss on the extension of the latter study on equations on co-evolving graphs. The talk is based on works in collaboration with G. Heinze (Augsburg), L. Mikolas (Oxford), F. S. Patacchini (IFP Energies Nouvelles), A. Schlichting (University of Münster), and D. Slepcev (Carnegie Mellon University).
Joaquín Fontbona: Quantitative large population limit for mean-field interacting branching diffusions
We establish an explicit rate of convergence for some systems of mean-field interacting diffusions with logistic binary branching, towards solutions of nonlinear evolution equations with non-local self-diffusion and logistic mass growth, describing their large population limit. The proof relies on a novel coupling argument for binary branching diffusions based on optimal transport, allowing us to sharply mimic the trajectory of the interacting branching population by means of a system of independent particles with suitably distributed random space-time births. We are thus able to derive an optimal convergence rate (in the dual bounded-Lipschitz distance on finite measures), for the empirical measure of the population, from the known convergence rate in 2-Wasserstein distance of empirical distributions of i.i.d. samples. Our approach and results extend propagation of chaos techniques and ideas from kinetic models, to stochastic systems of interacting branching populations, and appear to be new in this setting, even in the simple case of pure binary branching diffusions. Joint work with Felipe Muñoz-Hernandez.
Diogo Gomes: Numerical methods for price models
This talk explores price formation models in the context of mean-field games (MFG) and machine learning. We will highlight our work, including a mean-field game model addressing price formation in markets subject to random fluctuations, such as commodities whose production and supply are unpredictable. We will also cover the market-clearing problem in asset trading with stochastic supply, reflecting scenarios like electricity markets where dynamic pricing strategies counterbalance supply noise. Additionally, a significant focus will be on a novel machine learning approach that employs dual recurrent neural network architectures for modeling price formation under common noise conditions. This method tackles the complexity introduced by random supply, optimizing the model through adversarial training and offering a posteriori estimates for convergence, demonstrated through numerical experiments.
Dante Kalise: Feedback Control Synthesis for Interacting Particle Systems across Scales
Luca Nenna: Sticky-Schrödinger problem : from Large Deviation principle to JKO scheme
In this talk we consider the Sticky-Schrödinger problem, namely the minimisation of a relative entropy with respect to the sticky Brownian motion under marginal constraints. Roughly speaking the sticky brownian process is a stochastic process which behaves as a standard diffusions in the interior of the prescribed domain and when it hints the boundary it sticks following an intrinsic tangential diffusion. We carefully derive a large variation principle and identify the limit functional which turns out to be an Optimal Transport problem (OT) with a given cost $d_\nu$ , where $\nu$ is the tangential viscosity. Moreover this OT problem defines a distance between probability measures and in the special case of $d_{\infty}$ we study the associated JKO scheme.
This talk is based on joint works with Jean-Baptiste Casteras and Léonard Monsaigeon.
Li Wang: Variational methods for general nonlinear gradient flows
In this talk, I will introduce a general variational framework for nonlinear evolution equations with a gradient flow structure, which arise in material science, animal swarms, chemotaxis, and deep learning, among many others. Building upon this framework, we develop numerical methods that have built-in properties such as positivity preserving and entropy decreasing, and resolve stability issues due to the strong nonlinearity. I will specifically discuss how to leverage ideas from optimization and machine learning to overcome difficulties such as boundedness requirement, slow convergence, and high dimensionality.
Marie-Therese Wolfram: On Boltzmann mean field games for knowledge growth
In this talk I will discuss a Boltzmann mean field game (BMFG) for knowledge growth, that was originally introduced by the economists Lucas and Moll. In BMFG the evolution of the agent density with respect to their knowledge level is described by a Boltzmann equation. Agents increase their knowledge through binary interactions with others; their increase is modulated by the interaction and learning rate: Agents with similar knowledge learn more in encounters, while agents with very different levels benefit less from learning interactions. The optimal fraction of time spent on learning is calculated by a Bellman equation, resulting in a highly nonlinear forward-backward in time PDE system.
I will discuss different generalisations of this model, the existence of special solutions ensuring exponential growth of the overall economy as well as the qualitative behaviour of solutions. Furthermore I corroborate and illustrate our analytical results with computational experiments.
Joint work with M. Burger, L. Kanzler and A. Lorz.
Contributed Talks
Elisabetta Carlini: Lagrange-Galerkin/Semi-Lagrangian scheme schemes for Mean Field Games
We propose a numerical approximation of a mean-field game system with nonlocal couplings. The approximation is constructed by combining Lagrange-Galerkin techniques, for the FP equation, with semi-Lagrangian techniques, for the HJB equation. We prove a convergence theorem scheme in arbitrary spatial dimensions. We propose an implementable version with inexact integration and finally show some numerical simulations. Joint works with F.J. Silva, A. Zorkot.
Elisa Calzola: A high-order scheme for Mean Field Games
We propose a high-order numerical scheme for time dependent mean field games systems. The scheme, which is built by combining Lagrange-Galerkin and semi- Lagrangian techniques, is explicit, conservative, consistent, and stable for large time steps compared with the space steps. We provide a convergence analysis for the exactly integrated Lagrange-Galerkin scheme applied to the Fokker-Planck equation, and we propose an
implementable version with inexact integration. Finally, we validate the convergence rate of the high-order method proposed by numerical simulations of two Mean Field Games problems.
Jaime Cisternas: Numerical classification of structured light beams using optimal transport theory
Laser beams with spatial and/or polarization structure can be used for free-space and fiber communication links, among many possible technological applications. Recent research has shown that it is possible to measure most of the properties encoded in the laser beam and use it as an information channel. In this presentation we will show the effects of atmospheric turbulence on the received beams, and how the tools of Optimal Transport can overcome these distortions, allowing an optimal selection of beam properties and a more accurate detection of the information content.
Gonzalo Contador: Minimum Wasserstein distance transformations for discrete, summable p-value combination statistics
We introduce a comprehensive framework to adjust a discrete test statistic for improving its hypothesis testing procedure. The proposal minimizes the Wasserstein distance to a
null-approxi\-mating continuous distribution using an optimal transport map and subsequently adjusting the variance of the continuous distribution to match that of the transport map. This new approach yields an asymptotically consistent test that
significantly improves type I error control and enhances statistical power without requiring an exact null distribution calculation or sampling based approximations. The widely known mid-p and Lancaster’s mean- value chi-squared statistics for Fisher’s
combination are shown to be special cases of this optimal transport map.
Matías Delgadino: Phase transitions, logarithmic Sobolev inequalities, and uniform-in-time propagation of chaos for weakly interacting diffusions
In this talk, we discuss how phase transitions affect the time scale for which the mean field approximation of interacting diffusions is valid. This is done by studying the limit as the number particles go to infinity of the associated logarithmic Sobolev inequality.
Michel De Lara: Games in Product Form and Kuhn’s Equivalence
Theorem
Game theory offers a mathematical formalism to study strategic interactions. In such models of competition, information (who knows what and before whom) plays a
crucial role. In the fifties, H. W. Kuhn used trees to define a game in extensive
form (GEF); in a GEF, the information of a player is represented by a partition
of the player node moves. In the seventies, H. S. Witsenhausen used
agents, a product set and a product sigma-field to define the so-called intrinsic model (IM) in multi-agent stochastic control problems; in an IM, the information of an agent is represented by a subfield of the product sigma-field. In this talk, we introduce games in product form (GPF) as an alternative (based on IM) to GEF. We advocate the relevance of GPF for game theory by
- providing a case of game form that is playable, but that
cannot be written on a tree, - illustrating with examples the easiness and flexibility of GPF
to model games (Alice and Bob, principal-agent models), - discussing how to represent stochastic and Bayesian games
inside the GPF formalism.
Then, we stress that, by replacing what R. Aumann called the “cumbersome tree model” with a product set, GPF can naturally be decomposed with respect to subgroups of agents. Such potential for decomposition, be it hierarchical or parallel, is certainly relevant for computational methods. We illustrate its theoretical interest by providing a definition of perfect recall, of behavioral strategies “à la Aumann” and by proving a Kuhn’s Equivalence Theorem for GPF.
Mathias Dus: Numerical solution of Poisson partial differential equation in high dimension using two-layer neural networks
The aim of this article is to analyze numerical schemes using two-layer neural networks with infinite width for the resolution of the high-dimensional Poisson partial differential equation (PDE) with Neumann boundary condition. Using Barron’s representation of the solution with a probability measure defined on the set of parameter values, the
energy is minimized thanks to a gradient curve dynamic on the 2-Wasserstein space of the set of parameter values defining the neural network. Inspired by the work from Bach and Chizat, we prove that if the gradient curve converges, then the represented function is the solution of the elliptic equation considered. In contrast to previous works, the activation function we use here is not assumed to be homogeneous to obtain global convergence of the flow. Numerical experiments are given to show the potential of the method.
Link to the preprint : https://arxiv.org/abs/2305.09408
Adriano Festa: Hybrid games in route planning for sailing vessels and their mean field limit
In the last decades, the sport of sailing has experienced an increasing impact of new technologies, and notably of scientific computing. Among all computational problems relevant for sailing, we focus here on route planning and race strategy, i.e., the
optimization of the yacht route.
In the most typical and basic form, the route planning problem requires reaching a windward mark in minimum time within a variable wind field. According to the previous literature and experimental evidence, this problem is approached from a stochastic viewpoint, in which the wind field is modeled as having both a deterministic and a stochastic component, since even when we have a reliable forecast of its evolution, the wind field is typically affected by random fluctuations that represent a crucial
part of the problem.
We discuss the extension of the classic dynamic programming approach to hybrid control systems, where a continuous controller can switch between a finite collection of states, paying a cost of switching. This approach requires the resolution of a system of quasi-variational Hamilton-Jacobi inequalities that we propose to approximate via a semi-Lagrangian scheme obtained by the direct discretization of the dynamical programming principle. We discuss the application of such a framework to model a sailing boat navigation problem for the optimization of the strategic choices on a race course.
The model can be extended to the non-zero sum games, naturally including the presence of 3 or more players. For the number of players going to infinity, it is possible to introduce a new model as its mean-field limit. This is the case of very crowded races, where the interaction between many players would be impossible to model correctly with other techniques.
Rodrigue Lelotte: The dual charge method for the multimarginal optimal transport with Coulomb cost
The multimarginal optimal transport occurs in statistical physics as well as in quantum chemistry, where it is used to describe strongly correlated electrons. In the recent years, efforts have been put into fashioning efficient numerical methods to solve this problem,
which is notoriously hard to solve from a computational point of view. In this talk, I will introduce a specific discretisation, owning to the physical interpretation of the Kantorovich dual, to tackle this problem numerically in the case of Coulomb interaction.
Mircea Petrache: Sharp discrete isoperimetric inequalities in periodic graphs via discrete PDE and Semidiscrete Optimal Transport
We develop criteria based on a calibration argument via discrete PDE and semidiscrete optimal transport, for finding sharp isoperimetric inequalities of the form $(\#\Omega)^{d-1}\leq C(\#\partial\Omega)^d$ where $\Omega$ is a subset of vertices of a graph, and
$\partial\Omega$ is the edge-boundary of $\Omega$. We also find the optimum isoperimetric shapes $\Omega$. Our method is a new geometric discrete counterpart to Optimal Transport and ABP method proofs valid in the continuum isoperimetric problem. This answers a question from (Hamamuki 2014, DCG), surpassing the difficulties that appear in extending his work on rectangular grids, to general periodic graphs dual to
simplicial meshes of equal volume in Euclidean spaces. The strategy uses a new link between the discrete isoperimetric problem, and the theory Voronoi tessellations and Aleksandrov solutions from semidiscrete optimal transport, via an “cell problem”
directly linked to the proof of Minkowski’s famous characterization of convex polyhedra. This is joint work with Matías Gomez.
Student’s session
Jules Berry: Approximation and perturbations of stable solutions to a stationary mean field game system
In this talk we consider stable solutions, in the sense of Briani-Cardaliaguet, to a stationary second order mean field game system with local coupling and quadratic Hamiltonian. We first provide sufficient conditions for the existence of such stable solutions and prove that they are isolated in some Banach space. After re-expressing solutions of the MFG system as zeros of a nonlinear map F we show that stable solutions have the property that the Fréchet differential of F at the solution is an isomorphism in a large class of Banach spaces. We then consider three applications of this fact. First we prove some error estimates for
the finite element approximation of stable solutions. The finite element approximation of the stationary MFG system was studied by Osborne and Smears where the convergence of the method was proved without error estimates. We also obtain the convergence of Newton’s method both at continuous and discrete level. Finally we consider regular perturbations of the coupling and investigate the stability of solutions to the corresponding mean field game systems.
Théo Girard: Numerics and existence for generalized Hughes’ models
The Hughes’ model is a model for the dynamics of pedestrian flows. In the one dimensional case, it represents the evacuation of agents in a corridor through either one of the exits. This model couples two PDEs : a discontinuous-flux conservation law and an eikonal equation. After a brief review about what’s known on the subject, I will present an existence result for solutions to a class of Hughes related model in the one dimensional case. I will also present numerical schemes for this kind of problem, including modifications of the model accounting for constrained evacuation at exits.
Guillaume Mahey: Wasserstein and MMD penalizations for unbalanced optimal transport
In many applications, Unbalanced Optimal Transport, has been proven superior compared to classical Optimal Transport. It is more flexible in practice, since it replaces the hard marginal constraint by a soft marginal one. However, current choices of penalizations on the marginals (KL, TV, l2,…) compare distributions element wise and thus do not take into account the underlying geometries of the distributions. In this presentation, we will give typical scenarios where the standard approach results in poor transport solution. We then propose to address this problem by introducing a new type of penalization that takes into account the geometries of the spaces where the marginals are supported. Typically Wasserstein and MMD penalizations. We will conclude by giving a meaningful transport solutions for the toy examples given before.
Mason Pearce: An Application of Semi-Discrete Optimal Transport: Modelling Polycrystalline Materials
In this talk we look at an application of semi-discrete optimal transport to materials science, generating models of polycrystalline materials, for example steel. The microstructures of these materials play an important role in determining their material
properties. Techniques to model the microstructures are valuable when performing computational studies of material properties, for example in computational homogenisation. The microstructures can be represented as Laguerre tessellations, such tessellations arise naturally as solutions to semi-discrete optimal transport problems. In this talk we focus on generating Laguerre tessellations whose constituent Laguerre cells have prescribed volumes and centroids.
Fernanda Urrea: Analysing necessary optimality conditions for optimal control problems in Wasserstein spaces
We consider a measure-theoretical formulation in the form of a mean-field optimal control with regularization, terminal cost and a final time constraint on the state of the form functional inequalities. This framework is of particular interest for applications on deep
learning since it can be studied as a deterministic optimal control problem whose only source of uncertainty is the initial condition. We provide an overview of the mathematical aspects of such a formulation, and also a time- optimal version of this setting.